Contoh Soal Balok Statis Tertentu Mekanika Teknik

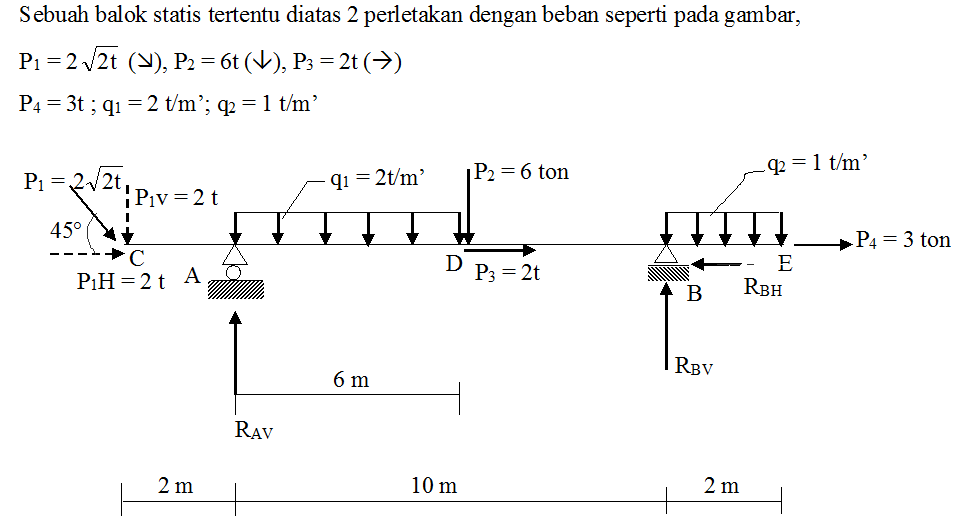
Diminta : Gambar bidang momen, gaya lintang dan bidang normal.(Bidang M, N, dan D)

Jawab :          Mencari reaksi vertical

Dimisalkan arah reaksi vertical di A=R_A  keatas dan arah reaksi vertical di B = R_B juga keatas.

Mencari R_AV = dengan SM_B = 0 (jumlah momen-momen terhadap titik B = 0)

Pemberian tanda pada persamaan berdasarkan atas arah momen, yang searah diberi tanda sama, sedang yang berlawanan arah diberi tanda berlawanan.

RBV à S MA = 0

Karena tanda R_BV adalah positif berarti arah reaksi R_BV sama dengan permisalan yaitu (Ó) keatas.

Untuk mengetahui apakah reaksi di A (R_A) dan reaksi di B (R_B) adalah benar, maka perlu memakai kontrol yaitu SV = 0

Mencari Raksi Horizontal

Karena perletakan A = rol à tidak ada R_AH.

Perletakan B = sendi à ada R_BH.

Untuk mencari R_BH dengan memakai syarat keseimbangan (SH = 0)

SH = 0

R_BH = P₁H + P₃ + P₄

      = 2 + 2 + 3 = 7 ton (Ñ)

Menghitung dan Menggambar Gaya Lintang (D)

Dihitung secara bertahap

Daerah C à A à lihat dari kiri

Gaya lintang dari C ke A bagian kiri adalah konstan

D_{A kr} = P1_{n =} - 2 ton (gaya lintang (D) di kiri titik A, di kiri potongan arah gaya lintang kebawah (Ô)

D_{A kn} (gaya lintang (D) di kanan titik A)

D_{A kn} = - P_{1n +} R_An = -2 + 13 = 11 ton (di kiri potongan arah gaya lintang ke atas).

Variabel x berjalan dari A ke D (sebelah kiri titik P2), sedang beban yang dihitung dimulai dari titik C.

Dx = -2 + 13 – q1 x   = (-P1V + RA – q1x)

Untuk x = 0 à    DAkn = -2 + 13 = + 11 ton

Untuk x = 6 m   à       DD kr= -2 + 13 – (2.6) = - 1ton (di kiri potongan arah gaya lintang ke bawah)

DD kn : sedikit di kanan titik D, melampaui beban P2.

DD kn : -2 + 13 – 12 – 6 = - 7 ton (dikiri potongan arah gaya lintang ke bawah)

Dari titik D s/d B tidak ada beban, jadi Bidang D sama senilai DD kn (konstan dari D sampai B).

Lebih mudah kalau dihitung dari kanan dari E menuju B.

Variabel x2 berjalan dari E ke B.

DE = 0

Dx2 = q2 . x2 = + x2 (persamaan liniear)

DB kn kanan perletakan B (x2 = 2 m)à DB kn = + 2 ton (kanan potongan arah ke 

kebawah)

DB kr  (kiri titik B) à  DB kr = + 2 – 9 = - 7 ton (kanan potongan arah ke atas)

MENGHITUNG DAN MENGGAMBAR BIDANG NORMAL (N)

Daerah C-D à dihitung dari kiri sampai D, P2 tidak termasuk dari C ke D nilai  gaya normal konstan.

ND kr = - P1H = - 2 ton (gaya normal menekan batang)

Daerah D-Bàdihitung dari kiri (beban yang dihitung mulai dari titik C, batang dari  D ke B nilai gaya normal konstan).

ND kn = (-2 – 2) ton = - 4 ton (gaya normal menekan batang)

NB kr = NDkn = - 4 ton

Daerah B-Eàdihitung dari kanan, dari E ke B nilai gaya normal konstan.

NB kn = + 3 ton (gaya normal menarik batang)

Kalau dihitung dari kiri, dimana gaya normal dihitung dari titik C.

Dari kiri à DBkn = (-4 + 7) t = + 3 ton (gaya normal menarik batang)

Menghitung dan Menggambar Bidang Momen (M)

Variabel x berjalan dari C ke A

Mx = - P_1v . x = - 2 x (linier)

Untuk x = 0 à Mc = 0

            x = 2 à M_A = - 2.2 = - 4 tm.

(momen P_1v . x  mengakibatkan serat atas tertarik    sehingga tanda negatif (-) ).

Gaya-gaya yang dihitung mulai dari titik C

MENCARI MOMEN MAXIMUM

Letak dimana harga Mmax = Letak dimana harga (D = 0)

x1 = 5.5 mà Mmax   = - ½ .2 (5.5)² + 11.5.5 – 4

   =  26.25 tm.

Mencari titik dimana M = 0

Mx₁        = - ½ .q₁.x₁² + 11 x₁ – 4 = 0

            = x₁² – 11 x₁  + 4 = 0

x₁ = 0.3756 m (yang dipakai)

x₁’ = 10.62 m (tidak mungkin)

Untuk x₁ = 6 à M_D = -36 + 66 – 4 = + 26 tm

Daerah E-B  (dihitung dari kanan, titik E ke titik B) variabel x₂ berjalan dari E ke B

Parabola

Mx2 = - ½ q2 x22

Untuk x2 = 0 à  ME = 0

Untuk x2 = 2 à  MB = - ½ . 1.4 = -2 tm